Volver a Guía
Ir al curso
CURSO RELACIONADO
Física 03
2025
TORTI
¿Te está ayudando la guía resuelta?
Sumate a nuestro curso, donde te enseño toda la materia de forma súper simple. 🥰
Ir al curso
FÍSICA 03 UBA XXI
CÁTEDRA TORTI
Unidad 1
1.
Con los vectores $\overrightarrow{\boldsymbol{A}}$ y $\overrightarrow{\boldsymbol{B}}$ de la Figura 1, use un dibujo a escala para obtener la magnitud y la dirección de:
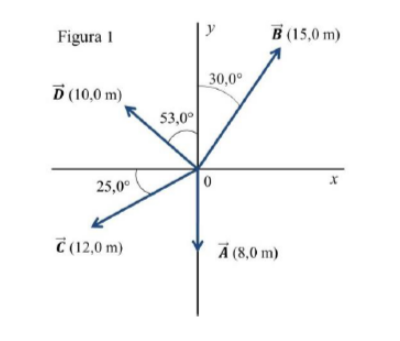
a) La suma vectorial de $\overrightarrow{\boldsymbol{A}}+\overrightarrow{\boldsymbol{B}}$ y la diferencia $\overrightarrow{\boldsymbol{A}}-\overrightarrow{\boldsymbol{B}}$.
a) La suma vectorial de $\overrightarrow{\boldsymbol{A}}+\overrightarrow{\boldsymbol{B}}$ y la diferencia $\overrightarrow{\boldsymbol{A}}-\overrightarrow{\boldsymbol{B}}$.
Respuesta
Sisi, ya voy yendo a buscar la hoja cuadriculada para hacer un dibujo a escala 🙄
Reportar problema
Vamos a hacerlo de manera analítica, ¿no? Conociendo para cada vector su módulo y en ángulo que forma con el eje $x$ o el eje $y$, podemos conocer las componentes en $x$ y en $y$ de estos vectores y calcular analíticamente la suma y resta que nos piden
Aclaración fuera de chiste: No es de vagancia que no hago el gráfico a escala a mano jaja si querés hacelo vos para convencerte, pero la manera en la que uno en general resolvería esto es analíticamente, tanto en Física como en Álgebra. Si nos queremos dar una idea gráfica de estos vectores, podemos usar GeoGebra. Pero para resolverlo sería muy poco práctico ponernos a graficar todo a mano y a escala siempre que querramos hacer una operación entre vectores. De hecho, así lo vamos a hacer en los ejercicios de parciales.
Una aclaración más: Todas las unidades están en metros
➡️ Vector A
El vector $A$ tiene módulo $8$ y sólo componente en $y$, apuntando en el sentido negativo. Lo escribimos así:
$\vec{A} = (0,-8)$
➡️ Vector B
El vector $B$ tiene módulo $15$ y forma un ángulo de $30°$ con el eje $y$. Usando trigonometría, como veíamos en la clase "✅ Descomposición de un vector. Coordenadas cartesianas y polares", las componentes $x$ e $y$ nos quedarían así:
$|B_x| = 15 \cdot \sin(30°) = 7.5$
$|B_y| = 15 \cdot \cos(30°) = 13$
Ambas componentes apuntan en el sentido positivo de los ejes, por lo que el vector $B$ nos quedaría así:
$\vec{B} = (7.5,13)$
Ahora sí, hacemos las operaciones que nos piden:
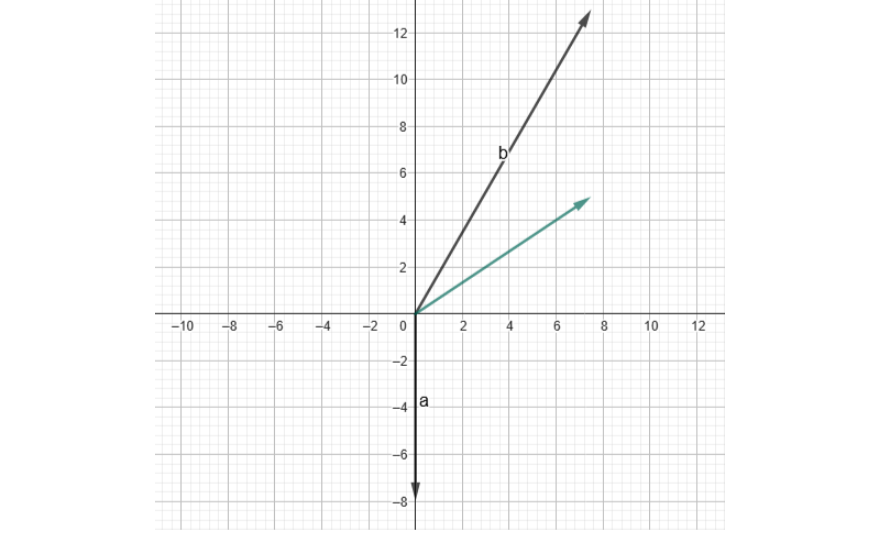
👉 $\vec{A} + \vec{B} = (0,-8) + (7.5,13) = (7.5, 5)$
Acá grafiqué la suma en GeoGebra (nuestra hoja a escala jejeje)
El módulo de este vector está dado por:
$|\vec{A} + \vec{B}| = \sqrt{7.5^2 + 5^2} = 9.01$
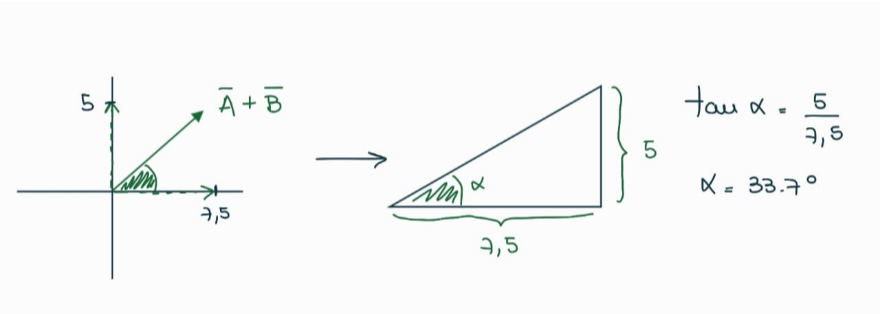
Y para dar la dirección, podemos encontrar el ángulo que forma el vector con el semieje positivo de las $x$, usando trigonometría:
Por lo tanto, la magnitud (el módulo) del vector $\vec{A} + \vec{B}$ es $9.01$ y forma un ángulo de $33.7°$ con el semieje positivo de las $x$
Vamos con la otra...
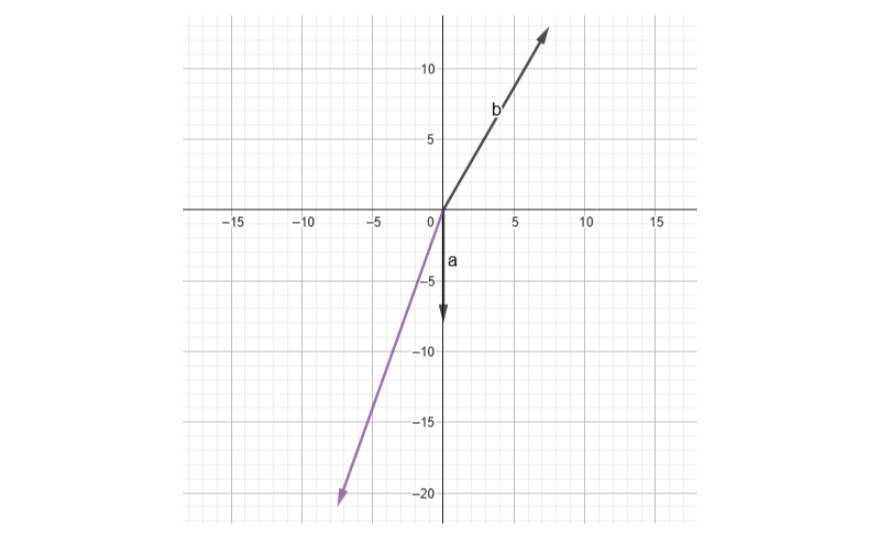
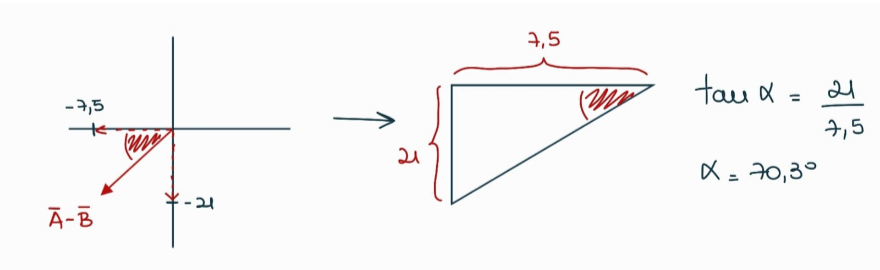
👉 $\vec{A} - \vec{B} = (0,-8) - (7.5,13) = (-7.5, -21)$
Gráficamente nos queda así:
El módulo de este vector está dado por:
$|\vec{A} - \vec{B}| = \sqrt{(-7.5)^2 + (-21)^2} = 22.3$
Para dar la dirección podemos encontrar este ángulo:
Por lo tanto, la magnitud (el módulo) del vector $\vec{A} - \vec{B}$ es $22.3$ y forma un ángulo de $70.3°$ con el semieje negativo de las $x$. También podríamos dar esta dirección a partir del del semieje positivo de las $x$, en ese caso le tenemos que sumar $180°$ (te das cuenta por qué? en el esquema de la izquierda, parate en el semieje positivo de las $x$ y andá en sentido antihorario hasta el vector... cuánto le tuviste que "agregar" a ese ángulo rojo?), así que este ángulo sería $250°$
Aclaración: En las respuestas de la guía pusieron el ángulo que forma con el semieje positivo de las $x$, pero no hay una única forma de dar esta dirección. Lo importante es que aclaremos ese ángulo respecto a qué.
💡 Importante: Acá en el curso, en la parte de ejercicios de parciales de vectores, muchas veces vamos a tener que dar la dirección del vector a partir de un ángulo, pero tranqui, en los enunciados de los parciales siempre te van a aclarar el ángulo respecto a qué (ejemplo, dar el ángulo respecto al semieje positivo de las $x$, respecto al semieje positivo de las $y$, etc...)
Iniciá sesión o
Registrate para
dejar
tu
comentario.
🤖 ExaBoti
Esta conversación es privada
🤖 ExaBoti (privado)